5. The Inverse Function and Invertibility

Inverse Function Definition:

Suppose f is a function with domain D and range R.
A function g is the inverse of f
if for all x in D and y in R the following holds:
f(x) = y ⟺ x = g(y)

Notation for Inverse Function: $f^{-1}$ Note: $f(f^{-1}(x))=x$ and $f^{-1}(f(x))=x$

Caution

The domain and range values may change depending on the type of equation.

Example:

$f(x)=\sqrt{x}$

The inverse of the function above would be…

$f^{-1}(x)=x^2\to Domain:[0,\infty )$

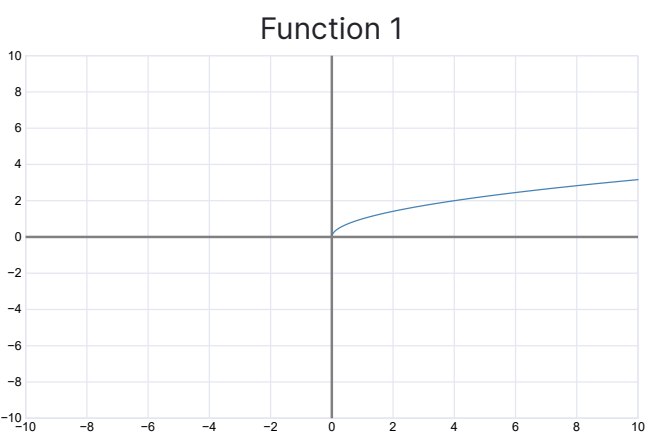
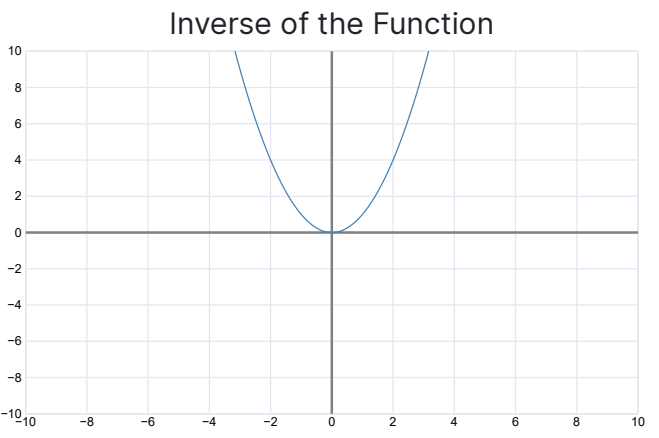
The two graphs have different domains. This is because we took the inverse function of a square root.

Invertibility:

Theorem

A function f is invertible, meaning an inverse function exists, precisely if it is one-to-one meaning.

Pertaining the above information… $f(x_1)\ne f(x_2)\to x_1\ne x_2$

Horizontal Line Test:

Theorem

A function is invertible if and only if all horizontal lines intersect the graph of the function in at most 1 place.

Transclude of HorizontalLineTest

Using the graph above, the horizontal line will not work because it will touch 2 areas. Therefore, the inverse of the graph above would become… $f(x)=\pm \sqrt{x}$ Therefore when $f(x)=x^2\to D=(-\infty ,0]$ the graph will show as the same curve but aligned horizontally. Graphs of an inverse is by reflecting the graph on the line y = x.

Case Study:

Given an invertible function $f(x)$ and a formula for this function there is a rather straightforward method to find a formula for the inverse function $f^{-}1(x)$. The method has three steps:

1. First we write down the equation $f(x)=y$;
2. Then we solve the equation for $x$ in terms of $y$;
3. Finally we substitute $y$ for $x$ and $x$ for $y$ to obtain the formula $y=f^{-}1(x)$. The best way to show how this method works is by example. So let’s consider the function $f(x)=x^2-2x+3$ on the domain $D=[1,\infty )$. You may check that the function is indeed invertible on this domain. To find the inverse we proceed with the steps as provided.

Step 1:

$x^2-2x+3=y$

Step 2:

$x^2-2x+3=y$ x^2-2x+3-y=0$$$$(x-1)^2+2-y=0 $(x-1{)}^2=y-2$ $x-1=\pm \sqrt{y-2}$ $x=1\pm \sqrt{y-2}$ Note that here we used the method of completing the square to solve a quadratic equation. You could also simply apply the quadratic (abc) formula $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ with $a=1$, $b=-2$ and $c=3-y$ to obtain this result. In order to finish solving the equation we should decide whether the square root comes with a plus or a minus sign. We decide this by considering the domain of the function $f(x)$. Indeed if we pick the minus sign then $x$ would be smaller than $1$ for each value of $y$ and therefore it would not be in the domain. Thus we must pick the plus sign, since in that case $x$ is in the domain of $f(x)$ for each value of $y$. So we find $x=1+\sqrt{y-2}$

Step 3:

If we interchange $x$ and $y$ we find that $y=1+\sqrt{x-2}$ and therefore $f^{-1}(x)=1+\sqrt{x-2}$ Final note: As a final note let us remark that there is no big mystery in step 3. It is merely included so that the formula for the inverse is again with the variable $x$ instead of $y$ simply because we like to use that letter to signify variables for functions.  You could perform that step at any point in the method, although it is convenient to do it as a last step.