4. Implicit Differentiation

Implicit Functions

Explicit Form:

• $y=3x^3\ln x$
• $y=\sin (x^2-4)$
• $y=\frac{x^5+7x^2}{x^2+1}$

Implicit Form:

• $x^3+y^3=6xy$
• $x^2+y^2=9$

An explicit formula is a function that expresses one variable as a function of the other, while an implicit formula represents a relationship between variables without expressing one variable in terms of the other.

For a function that passes the vertical line test, the slope of a tangent line to the curve can be found by explicit differentiation. For a function that does not pass the vertical line test, we can use implicit differentiation.

When we are finding the tangent line of a circle, we do not have an explicit formula. In this case, we can split the circle in half.

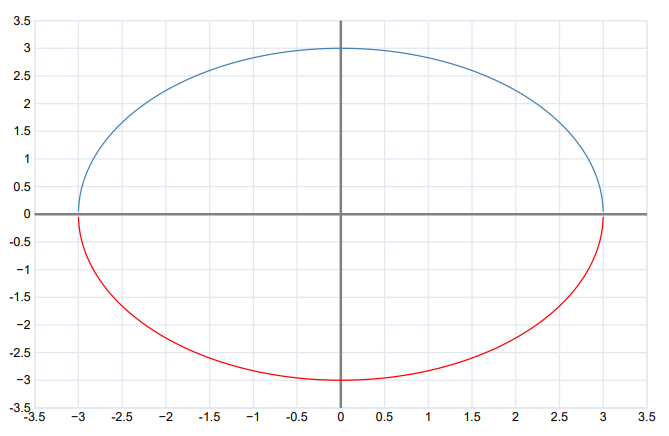
The circle above is split into 2 equations.

• $y=\sqrt{9-x^2}$
• $y=-\sqrt{9-x^2}$

The tangent of any of these equations would just be the derivative of the equation. Take the first equation as an example. $\frac{dy}{dx}=\frac{-x}{\sqrt{9-x^2}}$ For the lower half, it would be… $\frac{dy}{dx}=\frac{x}{\sqrt{9-x^2}}$

Implicit Differentiation

Equation of the circle: $x^2+y^2=9$ We can say that $y=y(x)$ as it is defined implicitly. $x^2+(y(x){)}^2=9$ by solving for the derivative using the chain rule… $2x+2y(x)y^{\prime }(x)=0$ rearranging this equation creates $2y(x)y^{\prime }(x)=-2x$ solving for $\frac{dy}{dx}$ $y^{\prime }(x)=\frac{-2x}{2y(x)}=-\frac{x}{y(x)}$ Lastly, it simplifies to $\frac{dy}{dx}=\frac{-x}{y}$ By applying this to the circle, we can get the 2 equations of the upper half and the lower half.

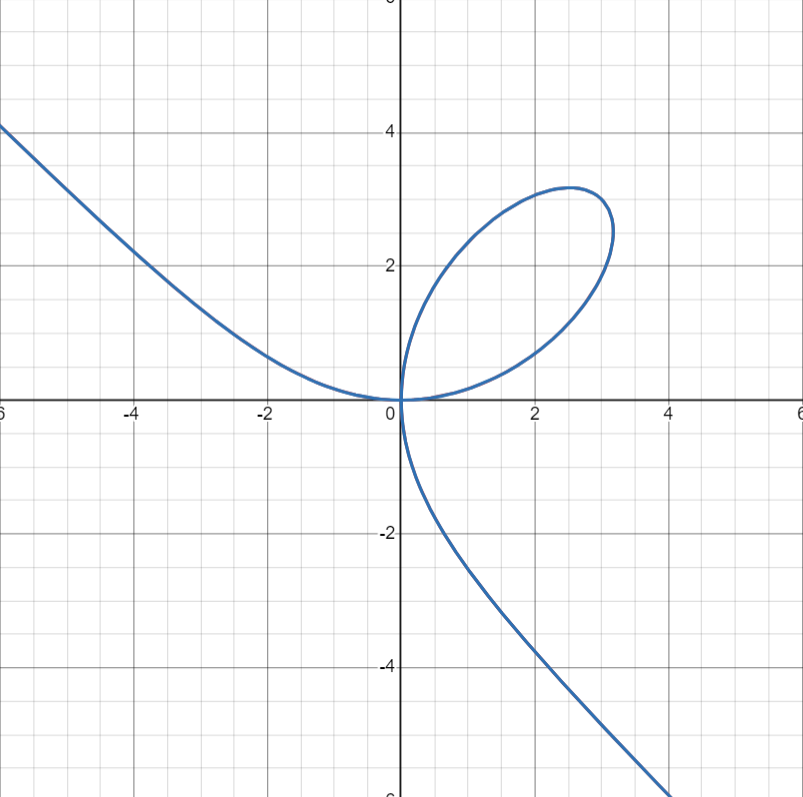
Another example can be used on the folium of Descartes. The equation is $x^3+y^3=6xy$ and when $y=y(x)$ is defined implicitly, $\frac{dy}{dx}=\frac{6y-3x^2}{3y^2-6x}$.