2. Introduction to Derivatives

Rate of Change

Definition

The rate of change of the function $y=f(x)$ over the interval $[a,b]$ is given by: $\frac{△y}{△x}=\frac{f(b)-f(a)}{b-a}$

Instantaneous Rate of Change

Definition

Letting the width $△x$ of the interval $[a,b]$ approach 0, the rate of change of the function $f(x)$ will approach the derivative $f^{\prime }(a)$ at the point of $a$: $f^{\prime }(a)={\lim }_{△x\to 0}\frac{△y}{△x}={\lim }_{b\to a}\frac{f(b)-f(a)}{b-a}$

Graph:

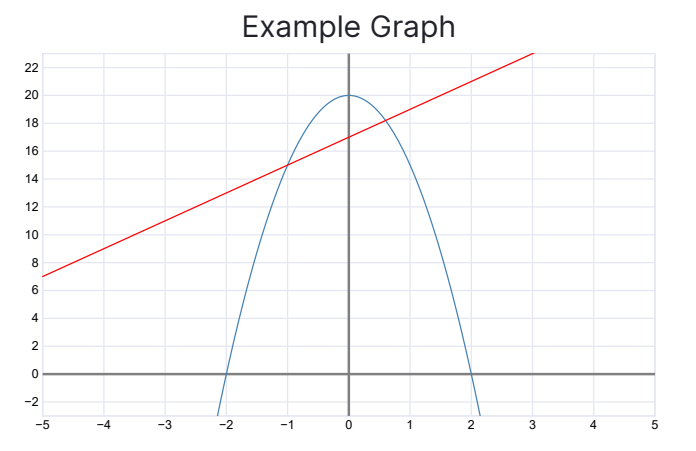
In this graph, if we keep on making the interval smaller and smaller, then the line will become a tangent. A tangent line has only 1 point touching the parabola line.

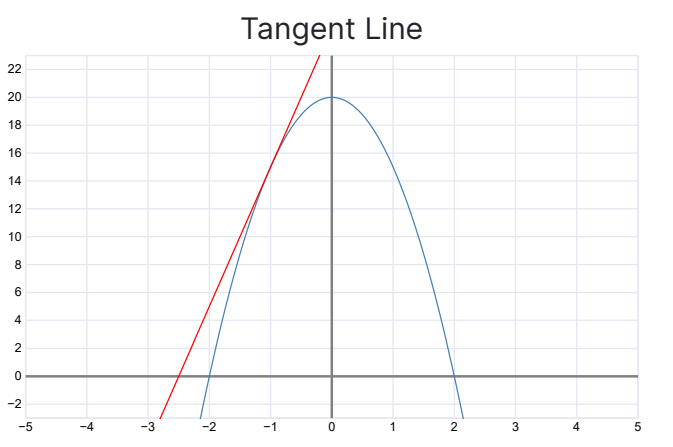
Definition

Given a function $f(x)$ the tangent line to the graph of $f$ at the point $a$ in the domain is given by the equation $y=f(a)+f^{\prime }(a)(x-a)$

Derivative at a Point

Definition

The slope of the tangent line to the function $f$ at the point $a$ is denoted by $f^{\prime }(a)$ or $\frac{df}{dx}(a)$ and called the derivative of $f$ at $a$.

There are some cases where a function doesn’t have a good differentiable point. There can be a “jump” which is where the graph breaks in the middle and jumps to another point and continues on. Or, there may be a “kink” where it looks like a v, similarly in absolute value graphs.

Derivative of a Function

Definition

Given a function $f:D\to R$ that is differentiable at each point $a$ in $D$ we define the derivative $f^{\prime }:D\to R$ as the function that associates the derivative of $f$ at $a$ to each point $a$ in the domain $D$.

Notation

The derivative of $f$ is also denoted $\frac{df}{dx}$. The second derivative $(f^{\prime }{)}^{\prime }=f^{\prime \prime }$ is also denoted $\frac{d^{2}f}{d{x}^2}$ The third derivative $(f^{\prime \prime }{)}^{\prime }=f^{(3)}$ is also denoted $\frac{d^{3}f}{d{x}^3}$ The nth derivative $f^{(n)}$ is also denoted $\frac{d^{n}f}{d{x}^n}$