2. Directional Derivatives

Interpretation

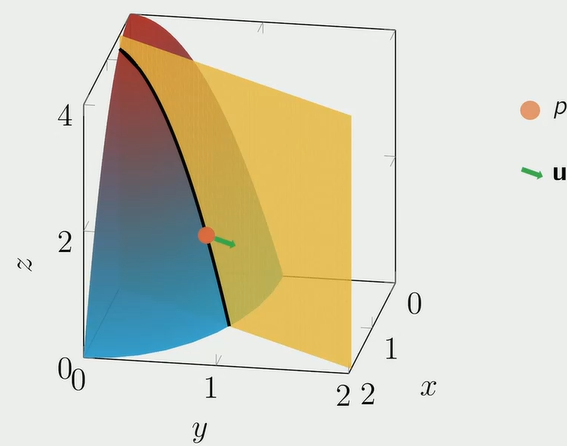
The image above consists of an interpretation of directional derivatives.

Information of $p$ and $u$

$p=(1,0.75)$

$u=⟨0.5,0.7⟩$

Partial Derivatives

Definition

Given a function $f(x,y)$ the partial derivative in the point $(a,b)$ are defined by $f_x(a,b)={\lim }_{h\to 0}\frac{f(a+h,b)-f(a,b)}{h}$ and $f_y(a,b)={\lim }_{h\to 0}\frac{f(a,b+h)-f(a,b)}{h}$

Directional Derivative

Definition

Given a function $f(x,y)$ and a unit vector $u=⟨u_1,u_2⟩$ the directional derivative in the point $(a,b)$ and in the direction $u$ is defined by

$D_{u}f(a,b)={\lim }_{h\to 0}\frac{f(a+u_{1}h,b+u_{2}h)-f(a,b)}{h}$

Unit Vector

Definition

Given a function $f(x,y)$ and a unit vector $u=⟨u_1,u_2⟩$ the directional derivative in the point $(a,b)$ and in the direction $u$ is defined by

$D_{u}f(a,b)={\lim }_{h\to 0}\frac{f(a+u_{1}h,b+u_{2}h)-f(a,b)}{h}$

Definition

A unit vector is a vector $u$ of length $||u||$ equal to 1.

Given a non-zero vector $u$ the normalized vector $\hat{u}=\frac{u}{||u||}$ is a unit vector with the same direction as $u$.

Relation with Partial Derivatives

Theorem

For a differentiable function $f(x,y)$ and a unit vector $u=⟨u_1,u_2⟩$ we have

$D_{u}f(a,b)=f_x(a,b)u_1+f_y(a,b)u_2$

at any point $(a,b)$.

Directional Derivative

Definition

Given a function $f(x_1,\dots ,x_n)$ and a unit vector $u=⟨u_1,\dots ,u_n⟩$ the directional derivative in the point $(a_1,\dots ,a_n)$ and in the direction $u$ is defined by

$D_{u}f(a_1,\dots ,a_n)={\lim }_{h\to 0}\frac{f(a_1+u_{1}h,\dots ,a_n+u_{n}h)-f(a_1,\dots ,a_n)}{h}$

Theorem

For a differentiable function $f(x_1,\dots ,x_n)$ and a unit vector $u=⟨u_1,\dots ,u_n⟩$ we have

$D_{u}f(a_1,\dots ,a_n)=f_{x_1}(a_1,\dots ,a_n)u_1+\cdots +f_{x_n}(a_1,\dots ,a_n)u_n$

Gradient Vector

Definition

Given a function $f(x_1,\dots ,x_n)$ the gradient vector $\nabla f$ at the point $(a_1,\dots ,a_n)$ is given by

$\nabla f(a_1,\dots ,a_n)=⟨f_{x_1}(a_1,\dots ,a_n),\dots ,f_{x_n}(a_1,\dots ,a_n)⟩$

Directional Derivative VS Gradient

Theorem

For a differentiable function $f(x_1,\dots ,x_n)$, a unit vector $u=⟨u_1,\dots ,u_n⟩$ and a point $p=(a_1,\dots ,a_n)$ we have

$D_{u}f(a_1,\dots ,a_n)=\nabla f(a_1,\dots ,a_n)\cdot u$