2. Double Integrals

Interpretation

Info

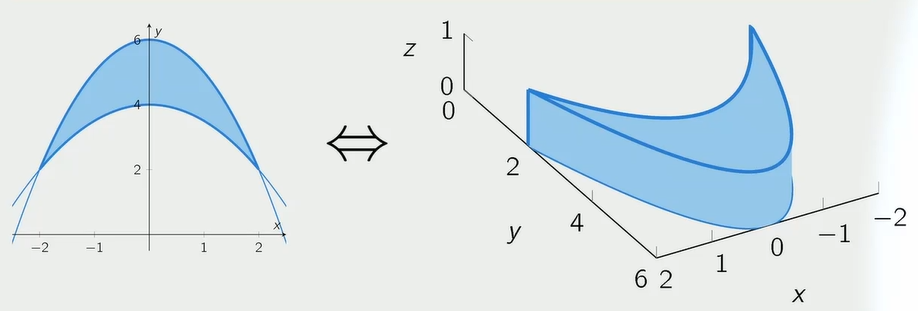
The double integral of $f$ over the region D, denoted by

${\iint }_{D}f(x,y)dA$

is the (signed) volume under the graph of $f$ for $(x,y)$ in $D$.

Riemann Integral

Definition

The integral of $f$ over the rectangle $R$ is

${\iint }_{R}f(x,y)dA={\lim }_{\nabla A\downarrow 0}{\sum }_{ij}f(x_{ij}^{\ast },y_{ij}^{\ast })△A$

if this limit exists.

Theorem

The double integral exists for any continuous function.

Computation Rules (Similar to Single Variable)

Theorem

• ${\iint }_{D}f(x,y)+g(x,y)dA={\iint }_{D}f(x,y)dA+{\iint }_{D}g(x,y)dA$
• ${\iint }_{D}cf(x,y)dA=c{\iint }_{D}f(x,y)dA$
• If $f(x,y)\le g(x,y)$ on $D$, then ${\iint }_{D}f(x,y)dA\le {\iint }_{D}g(x,y)dA$.

Theorem

• ${\iint }_{D}1dA=area(D)$

Theorem

If $D$ consists of non-overlapping parts $D_1,D_2$ then

• ${\iint }_{D}f(x,y)dA={\iint }_{D_1}f(x,y)dA+{\iint }_{D_2}f(x,y)dA$

---

In the video the mass and center of mass of a two dimensional object were introduced as important applications of double integrals. Another important application is the so-called moment of inertia of an object that rotates around an axis. This is the amount of torque needed for a desired angular rotation around this axis. For a point mass of mass $m$, the moment of inertia is given by $m{r}^2$, where $r$ is the distance to the rotational axis.

Suppose we now have a plate that occupies a region $D$ in the $xy$-plane with mass density function $\rho (x,y)$, which we rotate around the $x$-axis and we want to compute the moment of inertia, which we denote by $I_x$. The closest point on the $x$-axis to a given point $(x,y)$ is of course the point $(x,0)$. As such, the square of the distance of the point $(x,y)$ to the $x$-axis is given by $y^2$. Therefore, the contribution of a small rectangle with sides $△x$ and $△y$ around this point $(x,y)$ to the total moment of inertia is given by $y^2\rho (x,y)△x△y$. In order to compute the total moment of inertia around the $x$-axis, we need to add all of these contributions together and we find that

$I_x={\iint }_D{y}^2\rho (x,y)dxdy$

A similar formula holds for the moment of inertia around the $y$-axis, which we denote by $I_y$, and is given by

$I_y={\iint }_D{x}^2\rho (x,y)dxdy$

Finally, for rotation around the origin, the square of the distance of the point $(x,y)$ to the origin is given by $x^2+y^2$. So we find that the moment of inertia of rotation around the origin, which we denote by $I_0$, is given by

$I_0={\iint }_D(x^2+y^2)\rho (x,y)dxdy$